题目内容
△ABC中,AD⊥BC与D,且AB2=BC•BD,则△________∽△________;可以判定△ABC为________三角形.
ABD CBA 直角
分析:求出∠ADB=∠ADC=90°,求出 =
= ,根据∠B=∠B证△ABD∽△CBA,推出∠BAC=∠ADB=90°即可.
,根据∠B=∠B证△ABD∽△CBA,推出∠BAC=∠ADB=90°即可.
解答: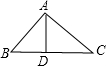
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB2=BC•BD,
∴ =
= ,
,
∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=∠ADB=90°,
∴△ABC是直角三角形,
故答案为:ABC,CBA,直角.
点评:本题考查了相似三角形的性质和判定的应用,主要考查学生的推理能力,注意:两边对应成比例,且夹角相等的两个三角形相似.
分析:求出∠ADB=∠ADC=90°,求出
 =
= ,根据∠B=∠B证△ABD∽△CBA,推出∠BAC=∠ADB=90°即可.
,根据∠B=∠B证△ABD∽△CBA,推出∠BAC=∠ADB=90°即可.解答:

∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB2=BC•BD,
∴
 =
= ,
,∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=∠ADB=90°,
∴△ABC是直角三角形,
故答案为:ABC,CBA,直角.
点评:本题考查了相似三角形的性质和判定的应用,主要考查学生的推理能力,注意:两边对应成比例,且夹角相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,△ABC中,AD平分∠BAC,BD⊥AD于D,点E是BC边的中点,AB=8,AC=12,求DE的长.
已知:如图,△ABC中,AD平分∠BAC,BD⊥AD于D,点E是BC边的中点,AB=8,AC=12,求DE的长. 如图,在△ABC中,AD平分∠BAC,AB=6,AC=4,△ABD的面积等于9.
如图,在△ABC中,AD平分∠BAC,AB=6,AC=4,△ABD的面积等于9.

 (2013•乌鲁木齐)如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为
(2013•乌鲁木齐)如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为