Question

【题目】如图，抛物线经过原点O（0，0），点A（1，1），点B（，0）．

（1）求抛物线解析式；

（2）连接OA，过点A作AC⊥OA交抛物线于C，连接OC，求△AOC的面积；

（3）点M是y轴右侧抛物线上一动点，连接OM，过点M作MN⊥OM交x轴于点N．问：是否存在点M，使以点O，M，N为顶点的三角形与（2）中的△AOC相似，若存在，求出点M的坐标；若不存在，说明理由．

Answer 1

【答案】（1）；（2）4；（3）（，﹣54）或（，）或（，﹣）

【解析】

（1）设交点式y=ax（x-），然后把A点坐标代入求出a即可得到抛物线解析式；

（2）延长CA交y轴于D，如图1，易得OA=，∠DOA=45°，则可判断△AOD为等腰直角三角形，所以OD=OA=2，则D（0，2），利用待定系数法求出直线AD的解析式为y=-x+2，再解方程组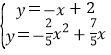，得C（5，-3），然后利用三角形面积公式，利用S△AOC=S△COD-S△AOD进行计算；

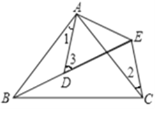
（3）如图2，作MH⊥x轴于H，AC=4，OA=，设M（x，-x2+x）（x＞0），根据三角形相似的判定，由于∠OHM=∠OAC，则当时，△OHM∽△OAC，即；当时，△OHM∽△CAO，即，则分别解关于x的绝对值方程可得到对应M点的坐标，由于△OMH∽△ONM，所以求得的M点能以点O，M，N为顶点的三角形与（2）中的△AOC相似．

（1）设抛物线解析式为y=ax（x-），

把A（1，1）代入得a1（1-）=1，解得a=-，

∴抛物线解析式为y=-x（x-），

即y=-x2+x；

（2）延长CA交y轴于D，如图1，

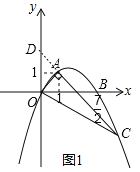
∵A（1，1），

∴OA=，∠DOA=45°，

∴△AOD为等腰直角三角形，

∵OA⊥AC，

∴OD=OA=2，

∴D（0，2），

易得直线AD的解析式为y=-x+2，

解方程组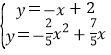得或，则C（5，-3），

∴S△AOC=S△COD-S△AOD=×2×5-×2×1=4；

（3）存在．如图2，

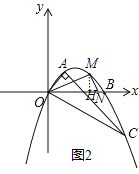
作MH⊥x轴于H，AC=，OA=，

设M（x，-x2+x）（x＞0），

∵∠OHM=∠OAC，

∴当时，△OHM∽△OAC，即，

解方程-x2+x =4x得x1=0（舍去），x2=-（舍去），

解方程-x2+x =-4x得x1=0（舍去），x2=，此时M点坐标为（，-54）；

当时，△OHM∽△CAO，即，

解方程-x2+x=x得x1=0（舍去），x2=，此时M点的坐标为（，），

解方程-x2+x=-x得x1=0（舍去），x2=，此时M点坐标为（，-）；

∵MN⊥OM，

∴∠OMN=90°，

∴∠MON=∠HOM，

∴△OMH∽△ONM，

∴当M点的坐标为（，-54）或（，）或（，-）时，以点O，M，N为顶点的三角形与（2）中的△AOC相似．