题目内容
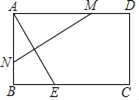
【题目】如图，在矩形纸片ABCD中，AB＝6，BC＝10，BC边上有一点E，BE＝4，将纸片折叠，使A点与E点重合，折痕MN交AD于M点，则线段AM的长是_____．
【答案】
【解析】
过M作MF⊥BC于F，根据矩形的性质得到∠DAB＝∠B＝90°，推出四边形ABFM是矩形，得到BF＝AM，FM＝AB＝6，根据折叠的性质得到AM＝ME，设AM＝
，则EF＝BF＝ ，根据勾股定理列方程即可得到结论．
过M作MF⊥BC于F，
∵四边形ABCD是矩形，
∴∠DAB＝∠B＝90°，
∴四边形ABFM是矩形，
∴BF＝AM，FM＝AB＝6，
∵将纸片折叠，使A点与E点重合，折痕MN交AD于M点，
∴AM＝ME，
设AM＝ ，则EF＝BF＝，
∴EF＝
，
在Rt△MEF中，
，
∴
，
解得：
.
故答案为： ．
练习册系列答案
阅读快车系列答案
相关题目
