题目内容
 如图所示,在梯形ABCD中,上底AD=1cm,下底BC=4cm,对角线BD⊥AC,交点为E,且BD=3cm,AC=4cm.
如图所示,在梯形ABCD中,上底AD=1cm,下底BC=4cm,对角线BD⊥AC,交点为E,且BD=3cm,AC=4cm.(1)求ABCD面积;
(2)求△BEC面积.
分析:(1)首先过点D作DF∥AC交BC的延长线于F点.易证得四边形ACFD为平行四边形.由BD⊥AC,即可得BD⊥DF,又由在Rt△BDF中,BD=3cm,DF=4cm,BF=5cm,即可求得BC边上的高,继而求得四边形ABCD面积;
(2)由AD∥BC,即可证得△ADE∽△CBE,然后由相似三角形的对应边成比例,求得BE与CE的长,继而求得△BEC面积.
(2)由AD∥BC,即可证得△ADE∽△CBE,然后由相似三角形的对应边成比例,求得BE与CE的长,继而求得△BEC面积.
解答: 解:(1)过点D作DF∥AC,交BC的延长线于F点.
解:(1)过点D作DF∥AC,交BC的延长线于F点.
∵AD∥BC,
∴四边形ACFD为平行四边形.
∴DF=AC=4cm,AC∥DF,CF=AD=1cm,
∴BF=BC+CF=4+1=5(cm),
∵AC⊥BD,
∴BD⊥DF,
在Rt△BDF中,BD=3cm,DF=4cm,BF=5cm,
∴BC边上的高h为:
=
(cm),
∴S四边形ABCD=
(AD+BC)h=
×(1+4)×
=6(cm2);
(2)∵AD∥BC,
∴△ADE∽△CBE,
∴
=
=
=
,
∴
=
,
=
,
∴DE=
cm,AE=
cm,
∴BE=3-DE=3-
=
(cm),EC=4-AE=
(cm),
S△BEC=
BE•EC=
×
×
=
(cm2).
 解:(1)过点D作DF∥AC,交BC的延长线于F点.
解:(1)过点D作DF∥AC,交BC的延长线于F点.∵AD∥BC,
∴四边形ACFD为平行四边形.
∴DF=AC=4cm,AC∥DF,CF=AD=1cm,
∴BF=BC+CF=4+1=5(cm),
∵AC⊥BD,
∴BD⊥DF,
在Rt△BDF中,BD=3cm,DF=4cm,BF=5cm,
∴BC边上的高h为:
| 3×4 |
| 5 |
| 12 |
| 5 |
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
(2)∵AD∥BC,
∴△ADE∽△CBE,
∴
| DE |
| BE |
| AE |
| EC |
| AD |
| BC |
| 1 |
| 4 |
∴
| DE |
| 3-DE |
| 1 |
| 4 |
| AE |
| 4-AE |
| 1 |
| 4 |
∴DE=
| 3 |
| 5 |
| 4 |
| 5 |
∴BE=3-DE=3-
| 3 |
| 5 |
| 12 |
| 5 |
| 16 |
| 5 |
S△BEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 5 |
| 12 |
| 5 |
| 96 |
| 25 |
点评:此题考查了相似三角形的判定与性质、梯形的性质、平行四边形的判定与性质以及直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
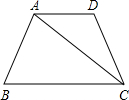 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.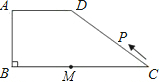 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有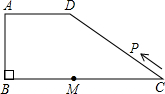 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.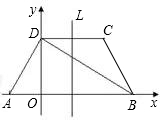 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )