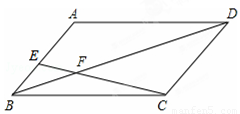
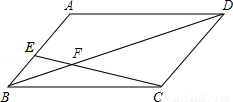
题目内容
在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.

考点:
菱形的判定;全等三角形的判定与性质;平行四边形的性质.
专题:
证明题.
分析:
(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF;
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行四边形,又DF=FB,可根据邻边相等的平行四边形为菱形证出结论.
解答:
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
 ,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.
点评:
此题主要考查了全等三角形的判定,以及菱形的判定,关键是掌握全等三角形的判定定理,以及菱形的判定定理,平行四边形的性质.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目