题目内容
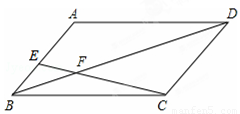
如图,在▱ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF=
【答案】

【解析】
试题分析:由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,继而可判定△BEF∽△DCF,根据相似三角形的对应边成比例,即可得BF:DF=BE:CD问题得解.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE:BE=4:3,
∴BE:AB=3:7,
∴BE:CD=3:7.
∵AB∥CD,
∴△BEF∽△DCF,
∴BF:DF=BE:CD=3:7,
即2:DF=3:7,
∴DF= .
.
考点: (1)相似三角形的判定与性质;(2)平行四边形的性质.

练习册系列答案
相关题目