题目内容
13.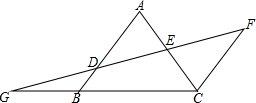 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.(1)求证:△ADE≌△CFE;
(2)若点D是GE的中点,求$\frac{BD}{AB}$的值.
分析 (1)求出∠A=∠FCE,根据全等三角形的判定推出即可;
(2)过E作EM∥BC,交AB于M,根据全等求出AE=EC,求出AM=BM=$\frac{1}{2}$AB,推出△MED∽△BGD,求出BD=DM=$\frac{1}{2}$BM=$\frac{1}{4}$AB,即可求出答案.
解答 (1)证明:∵AB∥FC,
∴∠A=∠FCE,
在△ADE和△CFE中,
$\left\{\begin{array}{l}{∠AED=∠FEC}\\{∠A=∠FCE}\\{DE=FE}\end{array}\right.$,
∴△ADE≌△CFE;
(2)解:过E作EM∥BC,交AB于M,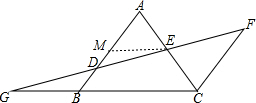
∵△ADE≌△CFE,
∴AE=EC,
∵ME∥BC,
∴AM=BM=$\frac{1}{2}$AB,
∵点D是GE的中点,
∴DG=DE,
∵EM∥BC,
∴△MED∽△BGD,
∴$\frac{DE}{DG}$=$\frac{MD}{DB}$,
∴BD=DM=$\frac{1}{2}$BM=$\frac{1}{4}$AB,
∴$\frac{BD}{AB}$=$\frac{1}{4}$.
点评 本题考查了全等三角形的性质和判定,相似三角形的性质和判定,平行线分线段成比例定理的应用,能综合运用定理进行推理是解此题的关键,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列四组线段中,不能构成直角三角形的是( )
| A. | 4,5,6 | B. | 3,4,5 | C. | 5,12,13 | D. | 7,24,25 |
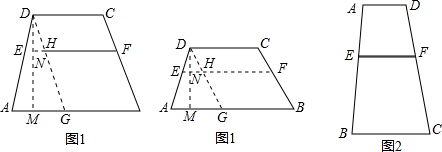 如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2.
如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2. 已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:
已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论: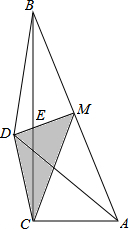 在△ABC中,AB=13,BC=12,CA=5,M是AB中点,点D与C在AB同侧,使DA=DB=7,则△CDM的面积为$\frac{357\sqrt{3}}{104}$.
在△ABC中,AB=13,BC=12,CA=5,M是AB中点,点D与C在AB同侧,使DA=DB=7,则△CDM的面积为$\frac{357\sqrt{3}}{104}$.