题目内容
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求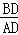 的值.
的值.
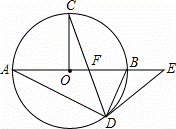
(1)证明:连结OD,如图,
∵EF=ED,
∴∠EFD=∠EDF,
∵∠EFD=∠CFO,
∴∠CFO=∠EDF,
∵OC⊥OF,
∴∠OCF+∠CFO=90°,
而OC=OD,
∴∠OCF=∠ODF,
∴∠ODC+∠EDF=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵OF:OB=1:3,
∴OF=1,BF=2,
设BE=x,则DE=EF=x+2,
∵AB为直径,
∴∠ADB=90°,
∴∠ADO=∠BDE,
而∠ADO=∠A,
∴∠BDE=∠A,
而∠BED =∠DAE,
=∠DAE,
∴△EBD∽△EDA,
∴ =
= =
= ,即
,即 =
= =
= ,
,
∴x=2,
∴ =
= =
= .
.


练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 图象的是( )
图象的是( )
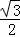 CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
CG2;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE的大小为定值.
 ÷(2+
÷(2+ ),其中a=
),其中a= .
. .
. B.
B. C.
C. D.
D.

 的结果是
的结果是 的图象上的概率是 .
的图象上的概率是 .