题目内容
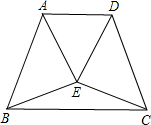已知等腰梯形ABCD，E为梯形内一点，且EA=ED．求证：EB=EC．
证明：∵EA=ED，
∴∠EAD=∠EDA．
∵等腰梯形ABCD，
∴∠BAE=∠CDE，AB=DC．
在△ABE和△DCE中
，
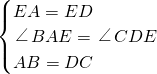∴△ABE≌△DCE．
∴EB=EC．
分析：欲证EB=EC，可证△ABE≌△DCE．
点评：本题主要考查全等三角形的判定和等腰梯形的性质．
∴∠EAD=∠EDA．
∵等腰梯形ABCD，
∴∠BAE=∠CDE，AB=DC．
在△ABE和△DCE中
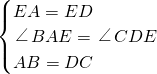，∴△ABE≌△DCE．
∴EB=EC．
分析：欲证EB=EC，可证△ABE≌△DCE．
点评：本题主要考查全等三角形的判定和等腰梯形的性质．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
3、如图，已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=8，则此等腰梯形的周长为（ ）
如图，已知等腰梯形ABCD的周长是20，AD∥BC，AD＜BC，∠BAD=120°，对角线AC平分∠BCD，则S梯形ABCD=
23、如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，点E为梯形外一点，且AE=DE．
如图，已知等腰梯形ABCD中，AB=CD，AD=