题目内容
8.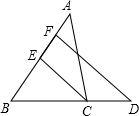 如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D三点在同一直线上,∠D=42°,当∠B的度数是多少时,EC∥FD?说明理由.
如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D三点在同一直线上,∠D=42°,当∠B的度数是多少时,EC∥FD?说明理由.
分析 此题可以采取倒推的思想,(将EC∥FD作为已知条件,来求∠B的度数),先根据两直线平行,同位角相等,即可得出∠BCE的度数,再根据角平分线的性质即可得出∠ACB的度数,再根据三角形的内角和定理即可求出∠B的度数.
解答 解:∵EC∥FD,
∴∠BCE=∠D=42°,
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°,
∵∠A+∠ACB+∠B=180°,
∴∠B=50°,
∴当∠B的度数是50度时,EC∥FD.
点评 此题考查了平行线的判定,解题的关键是:将问题中的EC∥FD作为已知条件,来求∠B的度数.

练习册系列答案
相关题目
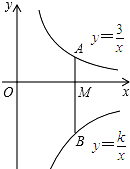 如图,点A在函数y=$\frac{3}{x}$(x>0)的图象上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,连接AB,AB垂直x轴于点M,且AM:MB=1:2,则k=-6.
如图,点A在函数y=$\frac{3}{x}$(x>0)的图象上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,连接AB,AB垂直x轴于点M,且AM:MB=1:2,则k=-6.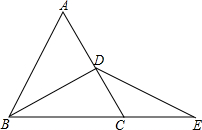 已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.
已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.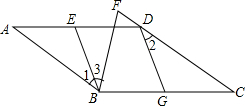 已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2. 如图,已知∠ACB=∠ADB=90°,N、M分别是AB、CD的中点,探究MN与CD的位置关系,并说明理由.
如图,已知∠ACB=∠ADB=90°,N、M分别是AB、CD的中点,探究MN与CD的位置关系,并说明理由.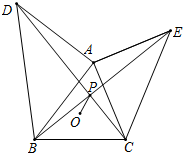 如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是5-$\frac{5}{3}\sqrt{3}$.
如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是5-$\frac{5}{3}\sqrt{3}$.