题目内容
 24、已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E.则AB平分∠DAE吗?请说明理由.
24、已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E.则AB平分∠DAE吗?请说明理由.分析:根据等腰三角形三线合一的性质可得到AD⊥BC,已知AD=AE,AE⊥BE,从而可根据HL判定△ABE≌△ABD,由全等三角形的性质可得到∠EAB=∠DAB,即AB平分∠DAE.
解答:解:平分.
∵AB=AC,点D是BC的中点
∴AD⊥BC
∵AD=AE,AE⊥BE,AB=AB
∴△ABE≌△ABD
∴∠EAB=∠DAB
∴AB平分∠DAE.
∵AB=AC,点D是BC的中点
∴AD⊥BC
∵AD=AE,AE⊥BE,AB=AB
∴△ABE≌△ABD
∴∠EAB=∠DAB
∴AB平分∠DAE.
点评:此题主要考查等腰三角形的性质及全等三角形的判定与性质的综合运用.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.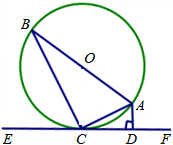 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.