题目内容
关于x的一元二次方程x2-2x+m=0有两个不相等的实数根,则整数m的最大值是 .
考点:根的判别式
专题:
分析:若一元二次方程有两不等实数根,则根的判别式△=b2-4ac>0,建立关于m的不等式,求出m的取值范围.
解答:解:∵一元二次方程x2-2x+m=0有两个不相等的实数根,
∴△=4-4m>0,
解得m<1,
故整数m的最大值为0,
故答案为0.
∴△=4-4m>0,
解得m<1,
故整数m的最大值为0,
故答案为0.
点评:考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
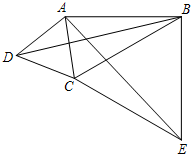 如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE. 如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=
如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1= 如图,在△ABC中,∠B与∠C的平分线交于点O.过O点作DE∥BC,分别交AB、AC于D、E.若AB=8,AC=6,则△ADE的周长是
如图,在△ABC中,∠B与∠C的平分线交于点O.过O点作DE∥BC,分别交AB、AC于D、E.若AB=8,AC=6,则△ADE的周长是 均匀地向一个如图所示的容器中注水,最后把容器注满,在注水过程中水面高度h随时间变化的函数图象大致是( )
均匀地向一个如图所示的容器中注水,最后把容器注满,在注水过程中水面高度h随时间变化的函数图象大致是( )


