题目内容
已知:抛物线![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)求证:抛物线与![]() 轴有两个交点;
轴有两个交点;
(2)设抛物线与![]() 轴的两个交点分别为
轴的两个交点分别为![]() 、
、![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴的交点为
轴的交点为![]() .
.
①当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
②将①中的抛物线沿![]() 轴正方向平移
轴正方向平移![]() 个单位(
个单位(![]() >0),同时将直线
>0),同时将直线![]() :
:![]() 沿
沿![]() 轴正方向平移
轴正方向平移![]() 个单位.平移后的直线为
个单位.平移后的直线为![]() ,移动后
,移动后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() .当
.当![]() 为何值时,在直线
为何值时,在直线![]() 上存在点
上存在点![]() ,使得△
,使得△![]() 为以
为以![]() 为直角边的等腰直角三角形?
为直角边的等腰直角三角形?
解:(1)证明:令![]() ,则
,则![]() .
.
△=![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ △![]() .
.
∴ 方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
∴ 抛物线与![]() 轴有两个交点.
轴有两个交点.
(2)①令![]() ,则
,则![]() ,
,
解方程,得![]() .
.
∵![]() 在
在![]() 左侧,且
左侧,且![]() ,
,
∴抛物线与![]() 轴的两个交点为
轴的两个交点为![]()
![]() ,
,![]()
![]() .
.
∵ 抛物线与![]() 轴的交点为
轴的交点为![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
在Rt△![]() 中,
中,![]() ,
,
![]() .
.
可得 ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ 抛物线的解析式为![]() .
.
②依题意,可得直线![]() 的解析式为
的解析式为![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
![]() .
.
∵ △![]() 为以
为以![]() 为直角边的等腰直角三角形,
为直角边的等腰直角三角形,
∴ 当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
∴ ![]() .
.
解得 ![]() 或
或![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
∴![]() .
.
解得![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
综上所述,![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
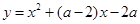 (
(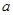 为常数,且
为常数,且 ).
).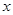 轴有两个交点;(3分)
轴有两个交点;(3分)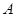 、
、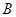 (
(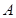 在
在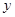 轴的交点为
轴的交点为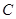 .
. 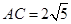 时,求抛物线的解析式;(3分)
时,求抛物线的解析式;(3分)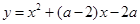 (
( 为常数,且
为常数,且 ).
).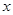 轴有两个交点;(3分)
轴有两个交点;(3分)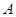 、
、 (
( 在
在 轴的交点为
轴的交点为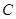 .
. 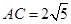 时,求抛物线的解析式;(3分)
时,求抛物线的解析式;(3分)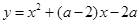 (
( 为常数,且
为常数,且 ).
).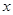 轴有两个交点;(3分)
轴有两个交点;(3分)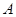 、
、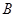 (
(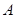 在
在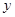 轴的交点为
轴的交点为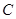 .
. 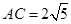 时,求抛物线的解析式;(3分)
时,求抛物线的解析式;(3分)