Question

2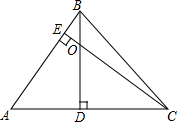．若∠BAC是△ABC的最大内角，△ABC的高BD、CE所在的直线相交于点O，点D、E都不与点A重合．猜想∠BAC和∠COD有何数量关系？请画出相应的图形，并证明你的结论．

Answer 1

分析 ①当△ABC为锐角三角形时，由∠ABD+∠A=90°，∠ABD+∠BOE=90°，得出∠A=∠BOE，再由∠BOE=∠COD，得出∠A=∠COD即可得出结论；
②当△ABC为直角三角形时，则D与A重合，不合题意舍去；
③△ABC为钝角三角形时，由∠ABD+∠COD=90°，∠ABD+∠BAD=90°，得出∠COD=∠BAD，再由∠BAD+∠BAC=180°即可得出结论．

解答 解：∠BAC和∠COD数量关系为：∠BAC=∠COD或∠BAC+∠COD=180°；理由如下：
分三种情况讨论：
①当△ABC为锐角三角形时，如图1所示：
∵CE⊥AB、BD⊥AC，
∴∠ABD+∠A=90°，∠ABD+∠BOE=90°，
∴∠A=∠BOE，
∵∠BOE=∠COD，
∴∠A=∠COD，
∴∠BAC=∠COD；
②当△ABC为直角三角形时，如图2所示：
则D与A重合，不合题意舍去；
③△ABC为钝角三角形时，如图3所示：
∵CE⊥BA、BD⊥AC，
∴∠ABD+∠COD=90°，∠ABD+∠BAD=90°，
∴∠COD=∠BAD，
∵∠BAD+∠BAC=180°，
∴∠COD+∠BAC=180°；
综上所述：∠BAC和∠COD数量关系为：∠BAC=∠COD或∠BAC+∠COD=180°．

点评 本题主要考查了三角形内角和定理、对顶角、邻补角等知识，根据不同三角形进行讨论是解决问题的关键．