题目内容
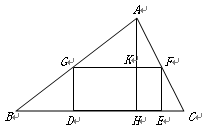
 如图,矩形DEFG的一组对边DE、GF截等边三角形ABC的两边AB、AC均成三等分,点G、F分别在AB、AC上,已知图中两个三角形(阴影部分)的面积和为
如图,矩形DEFG的一组对边DE、GF截等边三角形ABC的两边AB、AC均成三等分,点G、F分别在AB、AC上,已知图中两个三角形(阴影部分)的面积和为 ,则等边△ABC的边长为________.
,则等边△ABC的边长为________.
6
分析:设等边三角形的边长为3a.根据已知条件“DE、GF截等边三角形ABC的两边AB、AC均成三等分”求得HG=FI=a;然后根据两直线GF∥BC同位角相等及矩形的内角是90°求得∠DGH=30°,再在直角三角形中求得GD、DH的长度,从而求得S△DGH= a2;同理求得S△EFI=
a2;同理求得S△EFI= a2;最后根据“图中两个三角形(阴影部分)的面积和为
a2;最后根据“图中两个三角形(阴影部分)的面积和为 ”来解关于a的方程.注意a是正数.
”来解关于a的方程.注意a是正数.
解答: 解:设等边三角形的边长为3a.
解:设等边三角形的边长为3a.
∵DE、GF截等边三角形ABC的两边AB、AC均成三等分,
∴HG=FI=a;
∵GF∥BC,
∴∠AGF=∠ABC=60°,
∴∠DGH=90°-60°=30°;
∴DH= GH=
GH= a,GD=
a,GD= a;
a;
∴S△DGH= ×
× a×
a× a=
a= a2;
a2;
同理求得,S△EFI= ×
× a×
a× a=
a= a2;
a2;
∵S阴影=S△DGH+S△EFI= ,
,
∴ =
= a2+
a2+ a2,
a2,
解得,a=2或a=-2(不合题意,舍去),
∴3a=6,即等边三角形的边长为6.
故答案是:6.
点评:本题综合考查了矩形的性质(对边平行且相等,内角是90°)、平行线的性质(两直线平行,同位角相等)及直角三角形的解法.解答此题时,注意等边三角形的边长3a的取值范围3a>0,即a>0.
分析:设等边三角形的边长为3a.根据已知条件“DE、GF截等边三角形ABC的两边AB、AC均成三等分”求得HG=FI=a;然后根据两直线GF∥BC同位角相等及矩形的内角是90°求得∠DGH=30°,再在直角三角形中求得GD、DH的长度,从而求得S△DGH=
 a2;同理求得S△EFI=
a2;同理求得S△EFI= a2;最后根据“图中两个三角形(阴影部分)的面积和为
a2;最后根据“图中两个三角形(阴影部分)的面积和为 ”来解关于a的方程.注意a是正数.
”来解关于a的方程.注意a是正数.解答:
 解:设等边三角形的边长为3a.
解:设等边三角形的边长为3a.∵DE、GF截等边三角形ABC的两边AB、AC均成三等分,
∴HG=FI=a;
∵GF∥BC,
∴∠AGF=∠ABC=60°,
∴∠DGH=90°-60°=30°;
∴DH=
 GH=
GH= a,GD=
a,GD= a;
a;∴S△DGH=
 ×
× a×
a× a=
a= a2;
a2;同理求得,S△EFI=
 ×
× a×
a× a=
a= a2;
a2;∵S阴影=S△DGH+S△EFI=
 ,
,∴
 =
= a2+
a2+ a2,
a2,解得,a=2或a=-2(不合题意,舍去),
∴3a=6,即等边三角形的边长为6.
故答案是:6.
点评:本题综合考查了矩形的性质(对边平行且相等,内角是90°)、平行线的性质(两直线平行,同位角相等)及直角三角形的解法.解答此题时,注意等边三角形的边长3a的取值范围3a>0,即a>0.

练习册系列答案
相关题目
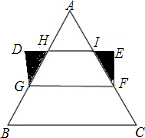 如图,矩形DEFG的一组对边DE、GF截等边三角形ABC的两边AB、AC均成三等分,点G、F分别在AB、AC上,已知图中两个三角形(阴影部分)的面积和为
如图,矩形DEFG的一组对边DE、GF截等边三角形ABC的两边AB、AC均成三等分,点G、F分别在AB、AC上,已知图中两个三角形(阴影部分)的面积和为 (2012•崇明县一模)已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF:GF=1:2,求矩形DEFG的周长.
(2012•崇明县一模)已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF:GF=1:2,求矩形DEFG的周长.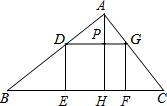 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.