题目内容
⊙O的半径r=5cm，圆心到直线l的距离OM=4cm，在直线l上有一点P，且PM=3cm，则点P（ ）
| A、在⊙O内 |
| B、在⊙O上 |
| C、在⊙O外 |
| D、可能在⊙O上或在⊙O内 |
考点：点与圆的位置关系
专题：
分析：由条件计算出OP的长度与半径比较大小即可．
解答：解：由题意可知△OPM为直角三角形，且PM=3，OM=4，
由勾股定理可求得OP=5=r，
故点P在⊙O上，
故选B．
由勾股定理可求得OP=5=r，
故点P在⊙O上，
故选B．
点评：本题主要考查点和圆的位置关系的判定，只要计算出P点到圆心的距离再与半径比较大小即可．
练习册系列答案
相关题目
如图，△ABC的顶点都在正方形网格格点上，点A的坐标为（-1，4）．将△ABC沿y轴翻折到第一象限，则点B的对应点B′的坐标是
如图所示，在四边形ABCD中，∠A=20°．直线l与边AB、AD分别相交于点M、N，则∠1+∠2=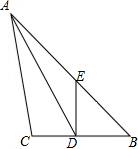
如图，在△ABC中，AD平分∠BAC，在AB上截取AE=AC，连结DE，已知DE=3.5cm，BD=4.5cm．