题目内容
 如图,在抛物线
如图,在抛物线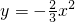 上取B1(
上取B1( ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为________.
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为________.
(0,-5050)
分析:首先求出A1、A2的坐标,通过观察得出规律,再根据规律求出A100的坐标.
解答:根据B1的坐标,易求得直线OB1的解析式为:y=- x;
x;
∵OB1A1是等边三角形,且B1(- ,-
,- ),
),
∴OA1=1,A1(0,-1);
∵直线OB1∥A1B2,又直线A1B2过点A1(0,-1),
∴直线A1B2的解析式为y=- x-1,联立抛物线的解析式,得:
x-1,联立抛物线的解析式,得:
 ,
,
解得: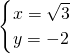 (x>0);
(x>0);
故B2( ,-2),A1A2=2,A2(0,-3);
,-2),A1A2=2,A2(0,-3);
同理可求得B3( ,-
,- ),A2A3=3,A3(0,-6);
),A2A3=3,A3(0,-6);
…
依此类推,当A100时,A99A100=100,
点A100纵坐标的绝对值=1+2+3+…+100=5050,
故A100(0,-5050).
点评:在解答此类规律型问题时,应该从简单的例子入手找出题目的一般化规律,然后根据规律求特定的值.
分析:首先求出A1、A2的坐标,通过观察得出规律,再根据规律求出A100的坐标.
解答:根据B1的坐标,易求得直线OB1的解析式为:y=-
 x;
x;∵OB1A1是等边三角形,且B1(-
 ,-
,- ),
),∴OA1=1,A1(0,-1);
∵直线OB1∥A1B2,又直线A1B2过点A1(0,-1),
∴直线A1B2的解析式为y=-
 x-1,联立抛物线的解析式,得:
x-1,联立抛物线的解析式,得: ,
,解得:
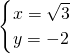 (x>0);
(x>0);故B2(
 ,-2),A1A2=2,A2(0,-3);
,-2),A1A2=2,A2(0,-3);同理可求得B3(
 ,-
,- ),A2A3=3,A3(0,-6);
),A2A3=3,A3(0,-6);…
依此类推,当A100时,A99A100=100,
点A100纵坐标的绝对值=1+2+3+…+100=5050,
故A100(0,-5050).
点评:在解答此类规律型问题时,应该从简单的例子入手找出题目的一般化规律,然后根据规律求特定的值.

练习册系列答案
相关题目
 上取点B1(
上取点B1( ,
, ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,,则A100的坐标为
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,,则A100的坐标为 
 上取B1(
上取B1( ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
 上取B1(
上取B1( ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
 上取B1(
上取B1( ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
 上取B1(
上取B1( ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,则A100的坐标为 .