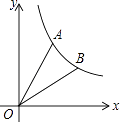题目内容
【题目】如图，抛物线y=﹣ 
x2+bx+c过点A（4，0），B（﹣4，﹣4）． 
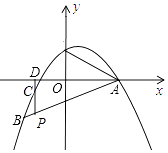
（1）求抛物线的解析式；
（2）若点P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交抛物线及x轴于C、D两点．请问是否存在这样的点P，使PD=2CD？若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】
（1）解：由题意 
，解得 
，
∴抛物线的解析式为y=﹣ 
x2+ 
x+2
（2）解：∵A（4，0），B（﹣4，﹣4），
∴直线AB的解析式为y= x﹣2，
设P（m， m﹣2），其中﹣4＜m＜4，则C（m，﹣ m2+ m+2），PD=2﹣ m，CD=|﹣ m2+ m+2|，
① 当点C在x轴上方时，CD=﹣ m2+ m+2，由PD=2CD，
得2﹣ m=2（﹣ m2+ m+2），解得m=﹣1或4（舍弃），
∴P（﹣1，﹣ 
）．
②当点C在x轴下方时，CD= m2﹣ m﹣2，由PD=2CD，得2﹣ m=2（ m2﹣ m﹣2），解得m=﹣3或4（舍弃），
∴P（﹣3，﹣ 
），
综上所述，点P的坐标为（﹣1，﹣ ）或（﹣3，﹣ ）
【解析】（1）利用待定系数法把问题转化为方程组解决．（2）设P（m， m﹣2），其中﹣4＜m＜4，则C（m，﹣ m2+ m+2），PD=2﹣ m，CD=|﹣ m2+ m+2|，分两种情形①当点C在x轴上方时，CD=﹣ m2+ m+2，由PD=2CD，得2﹣ m=2（﹣ m2+ m+2），②当点C在x轴下方时，CD= m2﹣ m﹣2，由PD=2CD，列出方程即可解决问题．
【考点精析】关于本题考查的二次函数的图象，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案．
