Question

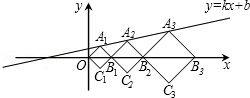在平面直角坐标系xOy中，正方形A₁B₁C₁O、A₂B₂C₂B₁、A₃B₃C₃B₂，…，按如图的方式放置，点A₁、A₂、A₃，…和点B₁、B₂、B₃，…分别在直线y=kx+b和x轴上，已知A₁（1，1），直线y=kx+b和x轴的夹角为15°，则正方形A₃B₃C₃B₂的面积是

 

；正方形A_nB_nC_nB_n-1的面积是

 

．

Answer 1

考点：一次函数综合题

专题：规律型

分析：根据正方形的轴对称性，由C₁、C₂的坐标可求A₁、A₂的坐标，将A₁、A₂的坐标代入y=kx+b中，得到关于k与b的方程组，求出方程组的解得到k与b的值，从而求直线解析式，由正方形的性质求出OB₁，OB₂的长，设B₂G=A₃G=b，表示出A₃的坐标，代入直线方程中列出关于b的方程，求出方程的解得到b的值，确定出A₃的坐标，确定出正方形A₃B₃C₃B₂的面积，依此类推寻找规律，即可求出A_n的坐标，得到正方形A_nB_nC_nB_n-1的面积．

解答：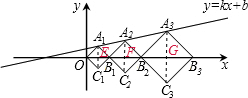
解：连接A₁C₁，A₂C₂，A₃C₃，分别交x轴于点E、F、G，
∵正方形A₁B₁C₁O、A₂B₂C₂B₁、A₃B₃C₃B₂，
∴A₁与C₁关于x轴对称，A₂与C₂关于x轴对称，A₃与C₃关于x轴对称，
∵C₁（1，-1），C₂（

7

2

，

3

2

），
∴A₁（1，1），即（5×（

3

2

）^1-1-4，（

3

2

）^1-1），A₂（

7

2

，

3

2

），即（5×（

3

3

）^2-1-4，（

3

2

）^2-1），
∴OB₁=2OE=2，OB₂=OB₁+2B₁F=2+2×（

7

2

-2）=5，
将A₁与A₂的坐标代入y=kx+b中得：

k+b=1 7 2 k+b= 3 2

，
解得：

k= 1 5 b= 4 5

，
∴直线解析式为y=

1

5

x+

4

5

，
设B₂G=A₃G=b，则有A₃坐标为（5+b，b），
代入直线解析式得：b=

1

5

（5+b）+

4

5

，
解得：b=

9

4

，
∴A₃坐标为（

29

4

，

9

4

），即（5×（

3

2

）^3-1-4，（

3

2

）^3-1），
此时正方形A₃B₃C₃B₂的面积是（

9

4

）²+（

9

4

）²=

2×81

16

=

2×32×3-2

22×3-2

；
依此类推A_n（5×（

3

2

）^n-1-4，（

3

2

）^n-1），正方形A_nB_nC_nB_n-1的面积（

3

2

）^2n-2+（

3

2

）^2n-2=

2×32n-2

22n-2

．
故答案为：

81

8

；

2×32n-2

22n-2

点评：此题属于一次函数综合题，正方形的性质，利用待定系数法求一次函数解析式，找出本题的规律是解本题的关键．