��Ŀ����
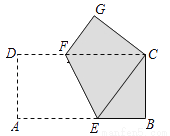
����ֽƬABCD�ı߳�AB=4��AD=2��������ֽƬ��EF�۵���ʹ��A���C�غϣ��۵�������һ����ɫ����ͼ��������ɫ���ֵ����Ϊ���٣�
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
��Ŀ����
����ֽƬABCD�ı߳�AB=4��AD=2��������ֽƬ��EF�۵���ʹ��A���C�غϣ��۵�������һ����ɫ����ͼ��������ɫ���ֵ����Ϊ���٣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�