Question

8．已知一次函数y=kx+b的图象经过点A（2，-1）和点B，其中点B是直线$y=-\frac{1}{2}x+3$与x轴的交点．
（1）求这个函数的表达式．
（2）在同一坐标系中，画出这两个函数的图象．

Answer 1

分析 （1）根据题意可得出B点坐标，结合A点坐标用待定系数法可求出函数解析式．
（2）根据两点法，画出函数的图象即可．

解答 解：（1）因为，当y=0时，得0=-$\frac{1}{2}$x+3，解得x=6，
所以，点B的坐标是（6，0）
又因为一次函数y=kx+b的图象经过点A（2，-1）和点B（6，0）
所以$\left\{\begin{array}{l}{2k+b=-1}\\{6k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=-\frac{3}{2}}\end{array}\right.$，
所以，这个函数的表达式为y=$\frac{1}{4}$x-$\frac{3}{2}$；
（2）在同一坐标系中，
画出这两个函数的图象，如图所示：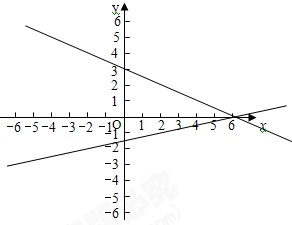

点评 此题考查了待定系数法求一次函数解析式，以及一次函数图象，熟练掌握待定系数法是解本题的关键．