题目内容
 如图,AB⊥BD,CD⊥BD,∠A+∠AEF=180°.求证:CD∥EF.
如图,AB⊥BD,CD⊥BD,∠A+∠AEF=180°.求证:CD∥EF.
某同学证法如下,请在横线上填写其推理过程或理由.
证明:因为AB⊥BD,CD⊥BD(________)
所以∠ABD=∠CDB=90°(________)
所以∠ABD+∠CDB=180°,
所以 AB∥(________)(________)
因为∠A+∠AEF=180°(________)
所以AB∥EF(________)
所以 CD∥EF(________)
已知 垂直的定义 CD 同旁内角互补,两直线平行 已知 同旁内角互补,两直线平行 同平行于一条直线的两直线平行
分析:先由AB⊥BD,CD⊥BD推出∠ABD+∠CDB=180°,即推出AB∥CD,再由∠A+∠AEF=180°推出AB∥EF,所以推出CD∥EF.
解答:证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB=90°(垂直定义)
∴∠ABD+∠CDB=180°
∴AB∥CD(同旁内角互补,两直线平行)
又∵∠A+∠AEF=180°(已知)
∴AB∥EF(同旁内角互补,两直线平行)
∴CD∥EF(同平行于一条直线的两直线平行)
故答案分别为:已知,垂直的定义,CD,同旁内角互补、两直线平行,已知,同旁内角互补、两直线平行,同平行于一条直线的两直线平行.
点评:此题考查的知识点是平行线的判定与性质,关键是先由AB⊥BD,CD⊥BD和已知∠A+∠AEF=180°根据同旁内角互补,两直线平行判定结论.
分析:先由AB⊥BD,CD⊥BD推出∠ABD+∠CDB=180°,即推出AB∥CD,再由∠A+∠AEF=180°推出AB∥EF,所以推出CD∥EF.
解答:证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB=90°(垂直定义)
∴∠ABD+∠CDB=180°
∴AB∥CD(同旁内角互补,两直线平行)
又∵∠A+∠AEF=180°(已知)
∴AB∥EF(同旁内角互补,两直线平行)
∴CD∥EF(同平行于一条直线的两直线平行)
故答案分别为:已知,垂直的定义,CD,同旁内角互补、两直线平行,已知,同旁内角互补、两直线平行,同平行于一条直线的两直线平行.
点评:此题考查的知识点是平行线的判定与性质,关键是先由AB⊥BD,CD⊥BD和已知∠A+∠AEF=180°根据同旁内角互补,两直线平行判定结论.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
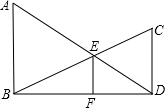 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明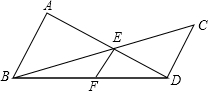
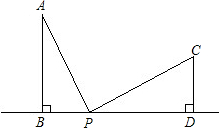 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动, 如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED. 如图,AB=BD,BC=BE,∠ABD=∠EBC,则有
如图,AB=BD,BC=BE,∠ABD=∠EBC,则有 如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.
如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.