题目内容
 已知在△ABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.试确定ED和BC的位置关系,并证明你的结论.
已知在△ABC中,AB=AC,D是AB上一点,延长CA至E,使AE=AD.试确定ED和BC的位置关系,并证明你的结论.考点:等腰三角形的性质
专题:
分析:根据等腰三角形的性质可得出∠B=∠C,∠E=∠ADE,根据对顶角相等可得∠BDF=∠ADE,再根据三角形外角的性质可得∠CFE=∠BFE,依此可得ED和BC的位置关系.
解答: 证明:延长ED交BC于F.
证明:延长ED交BC于F.
∵AB=AC,
∴∠B=∠C,
∵AE=AD,
∴∠E=∠ADE,
∵∠BDF=∠ADE,
∴∠CFE=∠BFE,
∴ED⊥BC.
 证明:延长ED交BC于F.
证明:延长ED交BC于F.∵AB=AC,
∴∠B=∠C,
∵AE=AD,
∴∠E=∠ADE,
∵∠BDF=∠ADE,
∴∠CFE=∠BFE,
∴ED⊥BC.
点评:本题考查了等腰三角形的性质,对顶角相等,三角形外角的性质和等量关系,需要熟练掌握.

练习册系列答案
相关题目
数轴上到-2点距离为3的点所表示的数是( )
| A、1或-5 | B、-5 |
| C、1 | D、以上都不对 |
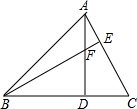 如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.