题目内容

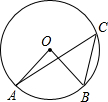如图：已知⊙O中，半径OA⊥OB，点A、B、C都在圆周上，则∠ACB=
45°
45°
．
分析：由两半径垂直，根据垂直定义得到两半径的夹角为90°，又根据所求的角与两半径的夹角所对的弧为同一条弧，根据圆周角定理：同弧所对的圆周角等于所对圆心角的一半，即可求出所求角的度数．
解答：解：∵OA⊥OB，
∴∠AOB=90°，
又圆心角∠AOB与圆周角∠ACB所对的弧都为
AB
，
∴∠ACB=
1
2
∠AOB=45°．
故答案为：45°
点评：此题考查了圆周角定理，圆周角定理的内容为：同弧所对的圆心角等于所对圆周角的2倍，其中弧是两角的联系点，故认真观察图形，找出圆心角与圆周角，建立已知角与未知角的联系是解本题的关键．
练习册系列答案
相关题目
如图，已知边长为3的正方形ABOC中，B，C两点分别在x轴正半轴，y轴的负半轴上，精英家教网过A点的双曲线y1=
kx
与直线AD：y2=ax+b的另一个交点D的纵坐标为1．
（1）求双曲线和直线AD的函数解析式；
（2）根据图象，写出x为何值时，y1＞y2？
如图①，已知：四边形OABC中，O为直角坐标系的原点，A点坐标为（1，4），B点在x轴的正半轴上，C点坐标为（8，-4），动点P从点O出发，依次沿线段OA、AB、BC向点C移动．设P点移动的路径为Z，△POC的面积S随着Z的变化而变化的图象如图②所示（其中线段DE∥x轴）．
精英家教网
（1）请你确定B点的坐标；
（2）当动点P是经过点O、B的抛物线的顶点时，
①求此抛物线的解析式；
②在x轴上是否存在点M，使△PBM与△OBC相似？若存在，请求出所有点M的坐标；若不存在，请说明理由．
（2012•苏州）如图，已知抛物线y=
1
4
x2-
1
4
（b+1）x+
b
4
（b是实数且b＞2）与x轴的正半轴分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C．
（1）点B的坐标为
（b，0）
（b，0）
，点C的坐标为
（0，
b
4
）
（0，
b
4
）
（用含b的代数式表示）；
（2）请你探索在第一象限内是否存在点P，使得四边形PCOB的面积等于2b，且△PBC是以点P为直角顶点的等腰直角三角形？如果存在，求出点P的坐标；如果不存在，请说明理由；
（3）请你进一步探索在第一象限内是否存在点Q，使得△QCO，△QOA和△QAB中的任意两个三角形均相似（全等可作相似的特殊情况）？如果存在，求出点Q的坐标；如果不存在，请说明理由．
（2012•中山一模）如图，已知等腰梯形ABCD的边BC在x轴上，点A（0，3）在y轴的正半轴上，点D的坐标为（2，3），且AB=
10
．
（1）求点B的坐标；
（2）求经过A、B、D三点的抛物线的解析式；
（3）在（2）中所求得的抛物线上是否存在点P，使得S△PBC=
2
3
S梯形ABCD？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．
如图，已知B（-1，0），C（1，0），A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F，且∠BDC=∠BAC．
（1）求证：∠ABD=∠ACD；
（2）求证：AD平分∠CDE；
（3）若在D点运动的过程中，始终有DC=DA+DB，在此过程中，∠BAC的度数是否变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网