题目内容
解关于x的方程:
(1)2x2-4x-1=0;
(2)x2-x-n2+n=0.
解:(1)∵a=2,b=-4,c=-1,
∴△=b2-4ac=16+8=24>0,
∴ ,
,
=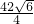 ,
,
= ,
,
∴x1= ,x2=
,x2= ;
;
(2)x2-x-n2+n=0.
∴(x-n)(x+n)-(x-n)=0,
∴(x-n)(x+n-1)=0,
∴x-n=0或x+n-1=0,
∴x1=n,x2=1-n.
分析:(1)利用公式法,首先确定△的符号,再利用公式直接求出两根即可,
(2)首先分解因式,利用两式相乘值为0,这两式中至少有一式值为0即可得出答案.
点评:此题主要考查了因式分解法和公式法解一元二次方程,只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程,难度适中.
∴△=b2-4ac=16+8=24>0,
∴
 ,
,=
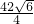 ,
,=
 ,
,∴x1=
 ,x2=
,x2= ;
;(2)x2-x-n2+n=0.
∴(x-n)(x+n)-(x-n)=0,
∴(x-n)(x+n-1)=0,
∴x-n=0或x+n-1=0,
∴x1=n,x2=1-n.
分析:(1)利用公式法,首先确定△的符号,再利用公式直接求出两根即可,
(2)首先分解因式,利用两式相乘值为0,这两式中至少有一式值为0即可得出答案.
点评:此题主要考查了因式分解法和公式法解一元二次方程,只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
解关于x的方程
=
产生增根,则常数m的值等于( )
| x-3 |
| x-1 |
| m |
| x-1 |
| A、-1 | B、-2 | C、1 | D、2 |