题目内容
如图所示,△ABC中,∠A=30°,AB=4,AC=6,P为AC上任一点(点P与点A,C都不重合),过点P作PD∥AB,交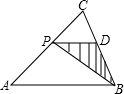 BC于D,设AP=x.
BC于D,设AP=x.
(1)求△BPD的面积S与x之间的函数关系式,并求出自变量x的取值范围;
(2)点P在AC上什么位置时,△BPD的面积最大,此时线段PD长度是多少?
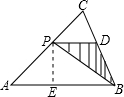
解:(1)过P作PE⊥AB于E.
∵PD∥AB
∴△CPD∽△CAB
∴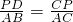 ,
,
即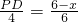 ,PD=
,PD= (6-x),
(6-x),
在Rt△APE中,∠A=30°,AP=x,
∴PE= x
x
S△BPD= •PD•PE
•PD•PE
= ×
× (6-x)×
(6-x)× x
x
=- x2+x(0<x<6);
x2+x(0<x<6);
(2)∵- <0,
<0,
∴函数有最大值.
当x=-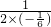 =3,即P为AC中点时,△BPD面积最大,此时PD的长为2.
=3,即P为AC中点时,△BPD面积最大,此时PD的长为2.
分析:(1)S△BPD= •PD•PE.分别用含x的式子表示PD、PE.在△APE中易表示PE;利用△CPD∽△CAB表示PD.
•PD•PE.分别用含x的式子表示PD、PE.在△APE中易表示PE;利用△CPD∽△CAB表示PD.
(2)运用函数性质求解.
点评:此题的关键是借助相似性表示PD与自变量x的关系,从而表达面积,得出函数关系式,然后运用函数性质求解.运用二次函数性质求最值常用公式法或配方法.
∵PD∥AB
∴△CPD∽△CAB
∴
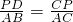 ,
,
即
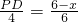 ,PD=
,PD= (6-x),
(6-x),在Rt△APE中,∠A=30°,AP=x,
∴PE=
 x
xS△BPD=
 •PD•PE
•PD•PE=
 ×
× (6-x)×
(6-x)× x
x=-
 x2+x(0<x<6);
x2+x(0<x<6);(2)∵-
 <0,
<0,∴函数有最大值.
当x=-
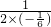 =3,即P为AC中点时,△BPD面积最大,此时PD的长为2.
=3,即P为AC中点时,△BPD面积最大,此时PD的长为2.分析:(1)S△BPD=
 •PD•PE.分别用含x的式子表示PD、PE.在△APE中易表示PE;利用△CPD∽△CAB表示PD.
•PD•PE.分别用含x的式子表示PD、PE.在△APE中易表示PE;利用△CPD∽△CAB表示PD.(2)运用函数性质求解.
点评:此题的关键是借助相似性表示PD与自变量x的关系,从而表达面积,得出函数关系式,然后运用函数性质求解.运用二次函数性质求最值常用公式法或配方法.

练习册系列答案
相关题目
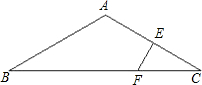 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=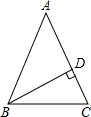 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.