题目内容
 如图,△ABC为等边三角形,D为BC边上一点,DE⊥AB于E,DF⊥AC于F,DE=19,DF=89,则△ABC的周长为
如图,△ABC为等边三角形,D为BC边上一点,DE⊥AB于E,DF⊥AC于F,DE=19,DF=89,则△ABC的周长为
- A.216
- B.216

- C.648
- D.324

B
分析:根据题意可得出∠BDE=∠CDF=30°,再由勾股定理可得出BD,CD,从而求出BC,再求出面积即可.
解答:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵DE⊥AB于E,DF⊥AC于F,
∴∠BED=∠CFD=90°,
设BE=x,CF=y,则BD=2x,CD=2y,
∵DE=19,DF=89,
∴BD=2× ,CD=2×
,CD=2× ,
,
∴BC= ,
,
∴△ABC的周长=3BC=216 .
.
故选B.
点评:本题考查了等边三角形的性质,勾股定理以及三角形的周长公式,解题的关键是求出一边的长.
分析:根据题意可得出∠BDE=∠CDF=30°,再由勾股定理可得出BD,CD,从而求出BC,再求出面积即可.
解答:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵DE⊥AB于E,DF⊥AC于F,
∴∠BED=∠CFD=90°,
设BE=x,CF=y,则BD=2x,CD=2y,
∵DE=19,DF=89,
∴BD=2×
 ,CD=2×
,CD=2× ,
,∴BC=
 ,
,∴△ABC的周长=3BC=216
 .
.故选B.
点评:本题考查了等边三角形的性质,勾股定理以及三角形的周长公式,解题的关键是求出一边的长.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=
16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=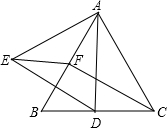 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE.
如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE. 如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.
如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.