题目内容
8.某超市经营一种小商品,进价为3.5元,据市场调查,销售单价是14.5元时平均每天销售量是500件,而销售价每降低1元,平均每天就可以多售出100件.(1)假定每件商品降价x元,商店每天销售这件商品的利润是y元,请写出y与x之间的关系式.
(2)每件商品售价是多少时,超市每天销售这种商品获得的利润最大?最大利润是多少?
分析 (1)根据等量关系“利润=(13.5-降价-进价)×(500+100×降价)”列出函数关系式.
(2)根据(1)中的函数关系式求得利润最大值.
解答 解:(1)设降价x元时利润最大、
依题意:y=(14.5-x-3.5)(500+100x),
整理得:y=-100(x-3)2+6400(0≤x≤11);
(2)由(1)可知,
∵a=-100<0,
∴当x=3时y取最大值,最大值是6400,
即降价3元时利润最大,
∴销售单价为11.5元时,最大利润6400元.
答:销售单价为11.5元时利润最大,最大利润为6400元
点评 考查了二次函数的应用,此题运用了数学建模思想把实际问题转化为数学问题.运用函数性质求最值常用公式法或配方法.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
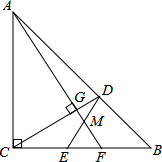 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E,F为线段BC上的两点,且CE=BF,连接AF,过点C作CD⊥AF于点G,交AB于点D,连接DE,交AF于点M.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E,F为线段BC上的两点,且CE=BF,连接AF,过点C作CD⊥AF于点G,交AB于点D,连接DE,交AF于点M. 如图,AO⊥BO,CO⊥DO,若∠AOC=α°,则∠BOD=α°.(用含α的式子表示)
如图,AO⊥BO,CO⊥DO,若∠AOC=α°,则∠BOD=α°.(用含α的式子表示)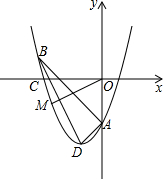 在某节习题课上,老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.
在某节习题课上,老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.