题目内容
如图，Rt△ABC中，∠B=90°，AB=5cm，AC=13cm，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于
- A.15cm
- B.16cm
- C.17cm
- D.18cm
C
分析：根据勾股定理求得BC=12cm，由题意得，AE=CE，则△ABE的周长等于AB+BE+AE=AB+BE+EC=AB+BC，即可求解．
解答：在Rt△ABC中，BC=
=
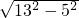=12cm，
由折叠过程可得，AE=CE，
则△ABE的周长等于AB+BE+AE=AB+BE+EC=AB+BC=5+12=17cm．
故选C．
点评：此题考查了勾股定理及图形的折叠的知识，折叠构成的全等图形是常用的隐含条件．
分析：根据勾股定理求得BC=12cm，由题意得，AE=CE，则△ABE的周长等于AB+BE+AE=AB+BE+EC=AB+BC，即可求解．
解答：在Rt△ABC中，BC=
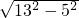==12cm，由折叠过程可得，AE=CE，
则△ABE的周长等于AB+BE+AE=AB+BE+EC=AB+BC=5+12=17cm．
故选C．
点评：此题考查了勾股定理及图形的折叠的知识，折叠构成的全等图形是常用的隐含条件．
练习册系列答案
相关题目
如图，Rt△ABC中，∠ACB=90°，tanB=
如图，Rt△ABC中，∠C=90°，BC=3，AC=4，若△ABC∽△BDC，则CD=（ ）
如图，Rt△ABC中，∠C=90°，△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F．
如图，Rt△ABC中，∠ABC=90゜，BD⊥AC于D，∠CBD=α，AB=3，BC=4．