题目内容
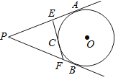
【题目】如图,![]() 、
、![]() 切
切![]() 于
于![]() 、
、![]() ,
,![]() 是弧
是弧![]() 上任一点,过点
上任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
![]() 若
若![]() ,求
,求![]() 的周长;
的周长;
![]() 若
若![]() ,
,![]() ,
,![]() ,你能求出
,你能求出![]() 的半径吗?
的半径吗?
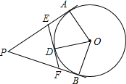
【答案】(1)8;(2)![]() 的半径是
的半径是![]() .
.
【解析】
(1)可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于PA+PB的结论;
(2)由(1)的结论可求出PA,PB的长,利用勾股定理的逆定理可判定△PEF是直角三角形,再利用切线的性质即可证明四边形DOBF是正方形,进而求出⊙O的半径.
(1)∵EA,ED都是圆O的切线,∴EA=ED,同理FD=FB,PA=PB,∴三角形PEF的周长=PE+PF+EF=PE+EA+PF+BF=PA+PB=2PA=8,即三角形PDE的周长是8;
(2)∵PE=13,PF=12.EF=5,∴PF2+EF2=PE2=169,∴△PEF是直角三角形,∴∠EFP=90°.
∵PA=PB=![]() ×△PEF周长,故有PA=PB=
×△PEF周长,故有PA=PB=![]() (13+12+5)=15,∴FB=PB﹣PF=15﹣12=3.
(13+12+5)=15,∴FB=PB﹣PF=15﹣12=3.
∵∠EFP=∠FDO=∠FBO=90°,OD=OB,∴四边形ODFB为正方形,∴OB=BF=3,即⊙O的半径是3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目