题目内容
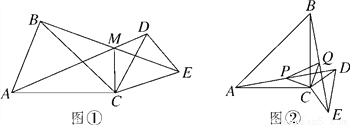
如图①，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，AD，BE相交于点M，连接CM.
(1)求证：BE＝AD；
(2)用含α的式子表示∠AMB的度数；
(3)当α＝90°时，取AD，BE的中点分别为点P，Q，连接CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明．
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
浙江之星学业水平测试系列答案高效智能课时作业系列答案题目内容
如图①，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，AD，BE相交于点M，连接CM.
(1)求证：BE＝AD；
(2)用含α的式子表示∠AMB的度数；
(3)当α＝90°时，取AD，BE的中点分别为点P，Q，连接CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明．
浙江之星学业水平测试系列答案高效智能课时作业系列答案
），商家按进价的3倍定价销售了一段时间后，为了吸引顾客，又在原定价的基础上打六折出售，那么按新的售价销售，每件童装所得的利润用代数式表示应为 元．
B. 
C. 
D. 
－
÷
＝__________.
;