题目内容
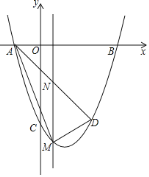
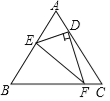
【题目】如图,等边![]() 的边长为10,点
的边长为10,点![]() ,
,![]() ,
,![]() 分别在三边
分别在三边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
根据等腰三角形的性质得到∠A=∠B=60°,∠DEF=60°,根据相似三角形的性质得到BE=2AD=6,AE=10-6=4,过E作EG⊥BF于G,解直角三角形得到BG=3,EG=![]() ,求得FG=5,根据勾股定理得到
,求得FG=5,根据勾股定理得到![]() =
=![]() ,所以
,所以![]() ;
;
如图,
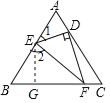
∵△ABC是等边三角形,
∴∠A=∠B=60°,
∵∠DEF=60°,
∴∠ADE=180°60°∠1,
∠2=180°∠160°,
∴∠ADE=∠2,
∴△ADE∽△BEF,
∴![]() ,
,
∵DF⊥DE,∠DEF=60°,
∴![]() 是直角三角形,∠EFD=30°,
是直角三角形,∠EFD=30°,
∴![]() ,
,
∴BE=2AD=6,
∴AE=10-6=4,
过E作EG⊥BF于G,
∵∠B=60°,BE=6,
∴BG=![]() ,
,![]() ,
,
∴FG=5,
∵![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ;
;

练习册系列答案
相关题目