Question

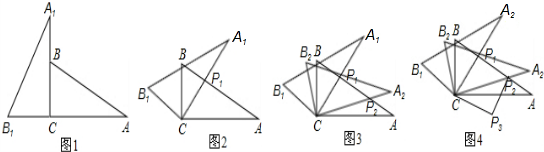
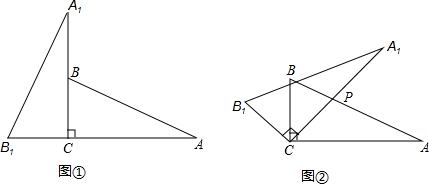
将两块含30°角且大小相同的直角三角板如图1摆放．

(1)将图1中△A₁B₁C绕点C顺时针旋转45°得图2，点P是A₁C与AB的交点，求证：CP₁＝AP₁；

(2)将图2中△A₁B₁C绕点C顺时针旋转30°到△A₂B₂C(如图3)，P₂是A₂C与AB的交点，线段CP₁与P₁P₂之间存在一个确定的等量关系，请你写出这个关系式并说明理由；

(3)将图3中线段CP₁绕点C顺时针旋转60°到CP₃(如图4)，连结P₃P₂，求证：P₃P₂⊥AB．

Answer 1

答案：
解析：

解：(1)过P1作P1M⊥AC于M，则∠PMC＝90°． 　　∠CP1M＝∠ACP1＝45°，CP1＝P1M，P1M＝AP1， 　　即CP1＝AP1． 　　(2)关系为：CP1＝P1P，过P作P1N⊥A2C于N，∠P2CA＝15°，∠P1P2C＝45°，则P1P2＝P1N，F1N＝CP，即CP1＝P1P2． 　　(3)由(2)知∠P1P2C＝45°，CP1＝CP3，∠P1CP2＝∠P3CP2，CP2＝CP2 　　∴△P1P2C≌△P3CP2，∠CP2P3＝∠CP2P3＝45° 　　∴∠P1P2P3＝∠P1P2C＋∠CP2P3＝90°， 　　∴P2P3⊥AB．