题目内容
【题目】如图，AB是垂直于水平面的建筑物．为测量AB的高度，小红从建筑物底端B点出发，沿水平方向行走了52米到达点C，然后沿斜坡CD前进，到达坡顶D点处，
．在点D处放置测角仪，测角仪支架DE高度为0.8米，在E点处测得建筑物顶端A点的仰角
为
（点A，B，C，D，E在同一平面内）．斜坡CD的坡度（或坡比）
，那么建筑物AB的高度约为（ ）
（参考数据
，
，
）
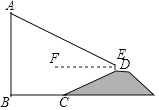
A.65.8米B.71.8米C.73.8米D.119.8米
【答案】B
【解析】
过点E作
与点M，根据斜坡CD的坡度（或坡比）
可设
，则
，利用勾股定理求出x的值，进而可得出CG与DG的长，故可得出EG的长．由矩形的判定定理得出四边形EGBM是矩形，故可得出
，
，再由锐角三角函数的定义求出AM的长，进而可得出结论．
解：过点E作与点M，延长ED交BC于G，
∵斜坡CD的坡度（或坡比），
米，
∴设
，则．
在
中，
∵
，即
，解得
，
∴
米，
米，
∴
米，
米．
∵，
，
，
∴四边形EGBM是矩形，
∴
米，
米．
在
中，
∵
，
∴
米，
∴
米．
故选B．
练习册系列答案
相关题目
