Question

有一块直角三角形纸片，两直角边AC=6cm，BC=8cm。

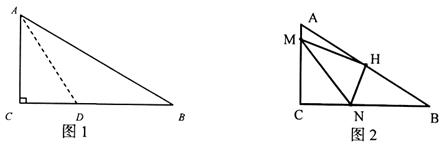
1.如图1，现将纸片沿直线AD折叠，使直角边AC落在斜边AB上，且与AB重合，则CD=             。

2.如图2，若将直角C沿MN折叠，使点C落在AB中点H上，点M、N分别在AC、BC上，则、与之间有怎样的数量关系？并证明你的结论。

 

Answer 1

 

1.3

2.答：

证明：过点B作BP//AC交MH延长线于点P，

∴A=PBH

在AMH和BPH中

A=PBH

AH=BH

AHM=BHP

∴AMH≌BPH

∴AM=BP，MH=PH

又∵NHMP

∴MN=NP

∵BP//AC，C=

∴NBP=

∴

∴

解析:（1）先根据勾股定理求出AB的长，设CD=xcm，则BD=（8-x）cm，再由图形翻折变换的性质可知AE=AC=6cm，DE=CD=xcm，进而可得出BE的长，在Rt△BDE中利用勾股定理即可求出x的值，进而得出CD的长．

（2）先证出AMH≌BPH，然后利用求出三角形NBP是直角三角形，再利用勾股定理求证。