题目内容
将一副三角板如图叠放，则△AOB与△DOC的面积比是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：因为AB∥CD，所以△AOB∽△DOC．欲求它们的面积比，必须先求出它们的相似比，以BC为中间值，利用直角三角形的性质来得到AB、CD的比值，从而根据相似三角形的面积比等于相似比的平方求得结果．
解答：解：∵AB∥CD，∴△AOB∽△COD；
根据题意，AB=BC，CD=
BC，即CD=
AB；
∴
=（
）2=
，故选C．
根据题意，AB=BC，CD=
| 3 |
| 3 |
∴
| S△AOB |
| S△DOC |
| AB |
| CD |
| 1 |
| 3 |
点评：考查了相似三角形的性质：面积比等于相似比的平方．
练习册系列答案
相关题目
将一副三角板如图叠放，则上下两部分面积S1：S2之比等于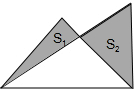
将一副三角板如图叠放，则左右阴影部分积之比
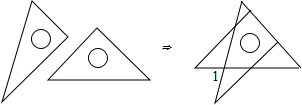（2013•凤阳县模拟）将一副三角板如图叠放，问∠1的度数为（ ）
将一副三角板如图叠放，设BC=1，则| BO |
| OD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|