题目内容
(1)求证:不论m为何值,关于x的方程2x(x-2m)=(1-m)(1+m)总有两个不等的实数根.
(2)二次函数y=2x2-4mx+m2-1的图象与x轴有交点吗?请说明理由.
(3)请你根据前两问得到的启示,利用二次函数y=2x2-4x+1的图象,求出x取何值时y>0.
(2)二次函数y=2x2-4mx+m2-1的图象与x轴有交点吗?请说明理由.
(3)请你根据前两问得到的启示,利用二次函数y=2x2-4x+1的图象,求出x取何值时y>0.
(1)原方程可化为:2x2-4mx+m2-1=0,
∵△=(-4m)2-4×2(m2-1)=8m2+8>0,
∴关于x的方程2x(x-2m)=(1-m)(1+m)总有两个不等的实数根;
(2)∵△=(-4m)2-4×2(m2-1)=8m2+8>0,
∴二次函数y=2x2-4mx+m2-1的图象与x轴总有两个不同的交点;
(3)∵二次函数y=2x2-4x+1中,a=2>0,
∴此函数的图象开口向上,
∵x=
=
=1±
,
∴二次函数y=2x2-4x+1的图象与x轴的交点为(1+
,0),(1-
,0),
∴当x>1+
或x<
时y>0.
∵△=(-4m)2-4×2(m2-1)=8m2+8>0,
∴关于x的方程2x(x-2m)=(1-m)(1+m)总有两个不等的实数根;
(2)∵△=(-4m)2-4×2(m2-1)=8m2+8>0,
∴二次函数y=2x2-4mx+m2-1的图象与x轴总有两个不同的交点;
(3)∵二次函数y=2x2-4x+1中,a=2>0,
∴此函数的图象开口向上,
∵x=
-b±
| ||
| 2a |
4±
| ||
| 2×2 |
| ||
| 2 |
∴二次函数y=2x2-4x+1的图象与x轴的交点为(1+
| ||
| 2 |
| ||
| 2 |
∴当x>1+
| ||
| 2 |
| ||
| 2 |

练习册系列答案
相关题目
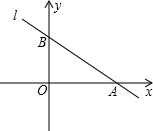 如图直线l:y=kx+2-4k(k为实数).
如图直线l:y=kx+2-4k(k为实数).