题目内容
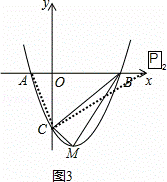
如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.

解:(1)∵二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴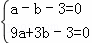 ,
,
解得: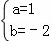 ,
,
则抛物线解析式为y=x2﹣2x﹣3;
(2)△BCM为直角三角形,理由为:
对于抛物线解析式y=x2﹣2x﹣3=(x﹣1)2﹣4,即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,即C(0,﹣3),
根据勾股定理得:BC=3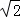 ,BM=2
,BM=2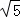 ,CM=
,CM=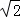 ,
,
∵BM2=BC2+CM2,
∴△BCM为直角三角形;
(3)如图1,
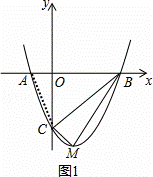
连接AC,
∵△COA∽△CAP,△PCA∽△BCD,
∴Rt△COA∽Rt△BCD,P点与O点重合,
∴点P(0,0).
如图2,过A作AP1⊥AC交y轴正半轴于P1,
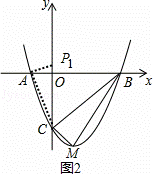
∵Rt△CAP1∽Rt△COA∽Rt△BCD,
∴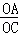 =
=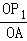 ,
,
即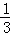 =
=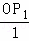 ,
,
∴点P1(0,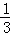 ).
).
如图3,过C作CP2⊥AC交x轴正半轴于P2,
∵Rt△P2CA∽Rt△COA∽Rt△BCD,
∴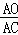 =
=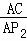 ,
,
即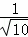 =
=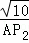 ,AP2=10,
,AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,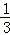 ),P2(9,0).
),P2(9,0).
点评: 此题是二次函数的综合题,涉及到二次函数解析式的确定、勾股定理、直角三角形的判定、相似三角形的判定和性质等知识,(3)题中能够发现点O是符合要求的P点,是解决此题的突破口.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 的绝对值是 ,
的绝对值是 ,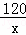 =
=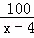 B.
B. 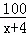 C.
C. 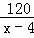 =
=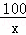 D.
D. 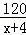 =
=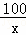
 ≈1.41,
≈1.41, ≈1.73.
≈1.73.

 B.
B.  C.
C.  D.
D. 
 B. 4或5 C. 5或6 D. 6
B. 4或5 C. 5或6 D. 6 .
.