题目内容
如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点.OA、OB的长度分别为a和b,且满足a2-2ab+b2=0.(1)判断△AOB的形状.
(2)如图②,正比例函数y=kx(k<0)的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.
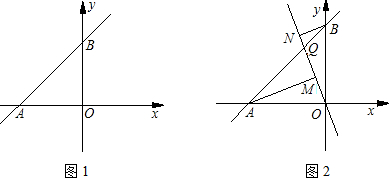
分析:(1)根据a2-2ab+b2=0,可得a=b,又有∠AOB=90°,所以可得出△AOB的形状;
(2)根据已知条件先证明△AOM≌△OBN,可得ON与OM的长,由MN=ON-OM即可得出答案.
(2)根据已知条件先证明△AOM≌△OBN,可得ON与OM的长,由MN=ON-OM即可得出答案.
解答: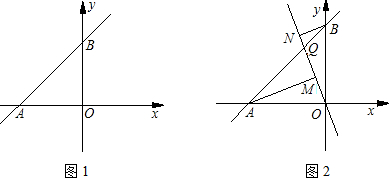 解:(1)∵OA、OB的长度分别为a和b,且满足a2-2ab+b2=0,∴a=b,
解:(1)∵OA、OB的长度分别为a和b,且满足a2-2ab+b2=0,∴a=b,
又∵∠AOB=90°,
∴△AOB为等腰直角三角形;
(2)∵AM⊥OQ,BN⊥OQ
∴∠AOM=∠OBN=90°-∠NOB
∴在△AOM和△OBN中
∴△AOM≌△OBN
∴ON=AM=9OM=BN=4(全等三角形对应边相等)
∴MN=ON-OM=9-4=5.
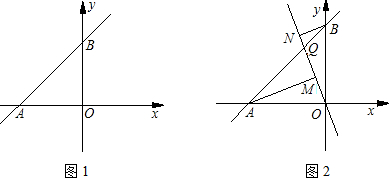 解:(1)∵OA、OB的长度分别为a和b,且满足a2-2ab+b2=0,∴a=b,
解:(1)∵OA、OB的长度分别为a和b,且满足a2-2ab+b2=0,∴a=b,又∵∠AOB=90°,
∴△AOB为等腰直角三角形;
(2)∵AM⊥OQ,BN⊥OQ
∴∠AOM=∠OBN=90°-∠NOB
∴在△AOM和△OBN中
|
∴△AOM≌△OBN
∴ON=AM=9OM=BN=4(全等三角形对应边相等)
∴MN=ON-OM=9-4=5.
点评:本题考查了一次函数的综合知识及全等三角形的判定,难度适中,关键是掌握三角形全等的判定方法.

练习册系列答案
相关题目

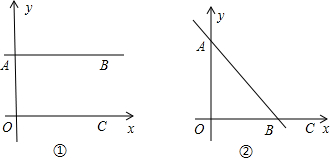
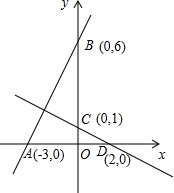 点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标.
点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标.
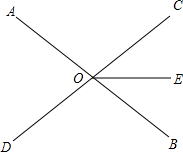 如图2,直线AB与CD相交于一点O,OE平分∠COB,且∠AOE=140°,则∠AOC=( )
如图2,直线AB与CD相交于一点O,OE平分∠COB,且∠AOE=140°,则∠AOC=( )