题目内容
【题目】已知
，
，
，斜边
，将绕点
顺时针旋转
，连接
.
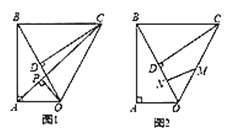
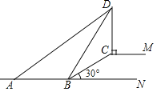
（1）如图，连接
，作
，垂足为
，求
的面积和线段
的长；
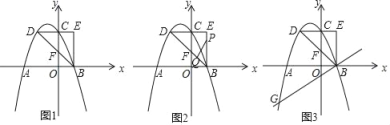
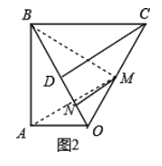
（2）如图，点
是线段
的中点，点
是线段
上的动点（不与点重合），求
周长的最小值.
【答案】（1）
，
；（2）最小值为
.
【解析】
（1）利用30°角的性质求出OA，AB，由旋转的性质得到
是等边三角形，根据勾股定理求出AC，再利用面积法可求出
面积和OP的值；
（2）如图2，连接BM，AM，根据等边三角形的性质得到BM⊥OC，根据全等三角形的性质得到BM=AB，AO=OM，得到AM被BD垂直平分，即M关于直线BO的对称点为A，连接AC，则C△CMN=AC+MC，于是得到结论．
解：（1）∵
，
，
∴
，
，
由旋转性质可知：
，
，∴是等边三角形，
∴
；
∴
，
，
∴
，
∴
，
∴
；
（2）如图2，连接
、
，
∵
为
中点，为等边三角形，∴
，
在
中，
，，
∴
，
∵，
∴
，
∵
，
，
∴
，
∴
，
，
∴
，
在的中垂线上，
∴被
垂直平分，
即关于直线
的对称点为
，
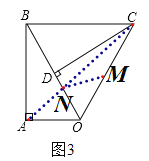
连接
，交
于点
，则此时
的周长最小，且
，
∵是的中点，
∴
，
∴
的最小值为.
练习册系列答案
相关题目
【题目】A城有肥料200吨，B城有肥料300吨．现要把这些肥料全部运往C，D两乡，从A城往C，D两乡运肥料的费用分别为20元/吨和25元/吨；从B城往C，D两乡运肥料的费用分别为15元/吨和24元/吨．现C乡需要肥料240吨，D乡需要肥料260吨．设从A城调往C乡肥料x吨.
(1)根据题意，填写下表：
调入地 数量/吨 调出地 | C | D |
A | x | ______ |
B | _____ | ______ |
总计 | 240 | 260 |
(2)给出完成此项调运任务最节省费用的调运方案及所需费用，并说明理由．
