题目内容
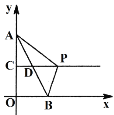
【题目】如图,在△ABC中,∠C=90°,点O、D分别为AB、BC的中点,做⊙O与AC相切于点E,在AC边上取一点F,使DF=DO.

⑴求证:DF是⊙O切线;⑵若sinB=![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
【答案】(1)证明略;(2)⊙O的半径![]() .
.
【解析】
(1)作OG⊥DF于G.连接OE.先证明△OGD≌△DCF得出OG=CD,再证明四边形CDOE是平行四边形,得出OG=OE即可解决问题;
(2)由FA,FD是⊙O的切线,推出FG=FE,设FG=FE=x,由△OGD≌△DCF(AAS),推出DG=CF=2,推出OD=DF=2+x,由AC=2OD,CE=OD,推出AE=EC=OD=2+x,由sinB=![]() 推出∠A=30°,推出
推出∠A=30°,推出![]() ,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题.
,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题.
(1)证明:作OG⊥DF于G.连接OE.

∵BD=DC,BO=OA,
∴OD∥AC,
∴∠ODG=∠DFC,
∵∠OGD=∠DCF=90°,OD=DF,
∴△OGD≌△DCF(AAS),
∴OG=CD,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠AEO=∠C=90°,
∴OE∥BC,
∵OD∥CE,
∴四边形CDOE是平行四边形,
∴CD=OE,
∴OG=OE,
∴DF是⊙O的切线.
(2)解:∵FA,FD是⊙O的切线,
∴FG=FE,设FG=FE=x,
∵△OGD≌△DCF(AAS),
∴DG=CF=2
∴OD=DF=2+x
∵AC=2OD,CE=OD,
∴AE=EC=OD=2+x
∵sinB=![]() .
.
∴∠B=60°,
∴∠A=30°,
![]()
在Rt△DCF中,∵DF2=CD2+CF2,

解得![]() 或
或![]()
![]()
即⊙O的半径是![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量的几组对应值如表:(注:日销售利润=日销售量×(销售单价﹣成本单价)
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
(1)求y关于x的函数解析式和m的值;
(2)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
【题目】近日,全省各地市的2019年初中毕业升学体育考试工作正依照某省教育厅的具体要求在有条不紊的进行当中,某中学在正式考试前,为了让同学们在中招体育考试中获得理想成绩,同时为了了解学生的当前水平,按批次进行了模拟考试,并随机抽取若干名学生问卷调查,现将调查结果绘制成如下不完整的统计图表:
组别 | 成绩范围x(分) | 频数(人数) |
A | 60<x≤70 | 54 |
B | 50<x≤60 | m |
C | 40<x≤50 | n |
D | 30<x≤40 | 6 |
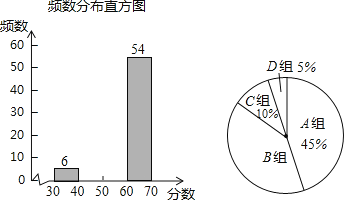
(1)这次调查的总人数有 人,表中的m= ,n= ;
(2)扇形统计图中B组对应的圆心角为 °;
(3)请补全频数分布直方图;
(4)若该校九年级共有学生2700名,且都参加了正式的初中毕业升学体育考试,小华也参加了这次考试并得了67分,若规定60分以上为优秀,体育老师想要在获得优秀的学生中随机抽出1名,作为学生代表向学弟学妹们传授经验,求抽到小华的概率.