题目内容
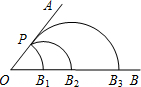 如图,点P为射线OA上一点,以点O为圆心,线段OP为半径画弧交OB于点B1,接着以点B1为圆心,线段PB1为半径画弧交OB于点B2,再以点B2为圆心,线段PB2为半径画弧交OB于点B3,构成一幅“海螺”图案,若∠AOB=52°,则弧PB3的度数是( )
如图,点P为射线OA上一点,以点O为圆心,线段OP为半径画弧交OB于点B1,接着以点B1为圆心,线段PB1为半径画弧交OB于点B2,再以点B2为圆心,线段PB2为半径画弧交OB于点B3,构成一幅“海螺”图案,若∠AOB=52°,则弧PB3的度数是( )分析:连接PB1、PB2,根据等边对等角的性质可得∠OPB1=∠OB1P,∠B1PB2=∠B1B2P,再根据等腰三角形两底角相等求出∠OB1P,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠B1B2P,然后根据平角的定义求出∠PB2B3,即可得弧PB3的度数.
解答: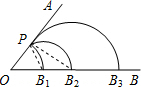 解:如图,连接PB1、PB2,
解:如图,连接PB1、PB2,
则OP=OB1,PB1=B1B2,
∴∠OPB1=∠OB1P,∠B1PB2=∠B1B2P,
∵∠AOB=52°,
∴∠OB1P=
(180°-∠OB1P)=
(180°-52°)=64°,
根据三角形的外角性质,∠B1B2P=
∠OB1P=
×64°=32°,
∴∠PB2B3=180°-∠B1B2P=180°-32°=148°,
即弧PB3的度数是148°.
故选D.
 解:如图,连接PB1、PB2,
解:如图,连接PB1、PB2,则OP=OB1,PB1=B1B2,
∴∠OPB1=∠OB1P,∠B1PB2=∠B1B2P,
∵∠AOB=52°,
∴∠OB1P=
| 1 |
| 2 |
| 1 |
| 2 |
根据三角形的外角性质,∠B1B2P=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PB2B3=180°-∠B1B2P=180°-32°=148°,
即弧PB3的度数是148°.
故选D.
点评:本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记等边对等角是解题的关键.

练习册系列答案
相关题目
 如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作
如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作 如图,点P在射线OM上,PC⊥OA,PD⊥OB,垂足分别为C,D且PC=PD,求证:OC﹦OD.
如图,点P在射线OM上,PC⊥OA,PD⊥OB,垂足分别为C,D且PC=PD,求证:OC﹦OD.
 9、如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(
9、如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(