Question

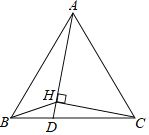
【题目】某地发生8.1级地震，震源深度20千米．救援队火速赶往灾区救援，探测出某建筑物废墟下方点C处有生命迹象．在废墟一侧某面上选两探测点A、B，AB相距2米，探测线与该面的夹角分别是30°和45°（如图）．试确定生命所在点C与探测面的距离．（参考数据≈1.41，≈1.73）

Answer 1

【答案】米.

【解析】

试题首先过C作CD⊥AB，设CD=x米，由题意可知，△CDB为等腰直角三角形，所以DB=CD=x米，在Rt△ACD中，根据∠CAD的正切可得AD=CD=x米，再根据AB=AD-BD可得方程x﹣x=2，解方程即可得生命所在点C与探测面的距离．

试题解析：解：过C作CD⊥AB，

设CD=x米，

∵∠ABE=45°，

∴∠CBD=45°，

∴DB=CD=x米，

∵∠CAD=30°，

∴AD=CD=x米，

∵AB相距2米，

∴x﹣x=2，

解得：x=．

答：生命所在点C与探测面的距离是米．