Question

【题目】如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

（1）直接写出D，E两点的坐标，D（　 　），E（　 　），直接判断四边形NMPE的形状为　 　；

（2）当t为何值时，四边形NMPE是正方形？

（3）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．

Answer 1

【答案】（1）（0，），（2，4），矩形；（2）t＝；（3）t＝或t＝2．

【解析】

（1）根据折叠的性质可知：AE＝OA，OD＝DE，那么可在直角三角形ABE中，用勾股定理求出BE的长，进而可求出CE的长，也就得出了E点的坐标．在直角三角形CDE中，CE长已经求出，CD＝OC﹣OD＝4﹣OD，DE＝OD，用勾股定理即可求出OD的长，也就求出了D点的坐标；

（2）根据四边形PMNE是个矩形，可用时间t表示出AP，PE的长，然后根据相似三角形APM和AED求出PM的长，根据正方形的性质列方程即可得到结论；

（3）本题要分三种情况进行讨论：（Ⅰ）ME＝MA时，此时MP为三角形ADE的中位线，那么AP＝ ，据此可求出t的值，过M作MF⊥OA于F，那么MF也是三角形AOD的中位线，M点的横坐标为A点横坐标的一半，纵坐标为D点纵坐标的一半．由此可求出M的坐标．

（Ⅱ）当MA＝AE时，先在直角三角形OAD中求出斜边AD的长，然后根据相似三角形AMP和ADE来求出AP，MP的长，也就能求出t的值．根据折叠的性质，此时AF＝AP，MF＝MP，也就求出了M的坐标；

（Ⅲ）EM＝EA的情况不成立．

解：（1）依题意可知，折痕AD是四边形OAED的对称轴，

∵在Rt△ABE中，AE＝AO＝5，AB＝4，BE＝ ＝3，

∴CE＝2，

∴E点坐标为（2，4），

在Rt△DCE中，DC2+CE2＝DE2，

又∵DE＝OD，

∴（4﹣OD）2+22＝OD2，

解得：OD＝ ．

∴D点坐标为（0，）．

∵PM∥DE，MN∥EP，

∴四边形NMPE为平行四边形．

又∵∠DEA＝90°，

∴四边形PMNE为矩形；

故答案为：（0，），（2，4），矩形；

（2）∵PM∥ED，

∴△APM∽△AED．

∴ ＝ ，

∴PM＝ ．

又∵AP＝t，ED＝ ，AE＝5，

∴PM＝ ＝ ，

当PM＝PE时，四边形NMPE是正方形，

即＝5﹣t，

解得：t＝ ，

当t＝时，四边形NMPE是正方形；

（3）（Ⅰ）若以AE为等腰三角形的底，则ME＝MA（如图①）

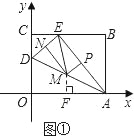
在Rt△AED中，ME＝MA，

∵PM⊥AE，

∴P为AE的中点，

∴t＝AP＝ AE＝ ，

又∵PM∥ED，

∴M为AD的中点，

过点M作MF⊥OA，垂足为F，则MF是△OAD的中位线，

∴MF＝OD＝ ，OF＝OA＝ ，

∴当t＝时，（0＜＜5），△AME为等腰三角形，

此时M点坐标为（， ）；

（Ⅱ）若以AE为等腰三角形的腰，则AM＝AE＝5（如图②）

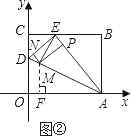
在Rt△AOD中，AD＝ ＝ ＝ ，

过点M作MF⊥OA，垂足为F，

∵PM∥ED，

∴△APM∽△AED，

∴，

∴t＝AP＝ ，

∴PM＝ t＝ ，

∴MF＝MP＝，OF＝OA﹣AF＝OA﹣AP＝5﹣2，

∴当t＝2时，（0＜2＜5），此时M点坐标为（5﹣2，）

（Ⅲ）根据图形可知EM＝EA的情况不成立，

综合综上所述，当t＝ 或t＝2时，以A，M，E为顶点的三角形为等腰三角形，相应M点的坐标为（， ）或（5﹣2，）．