题目内容
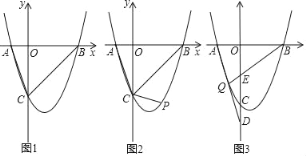
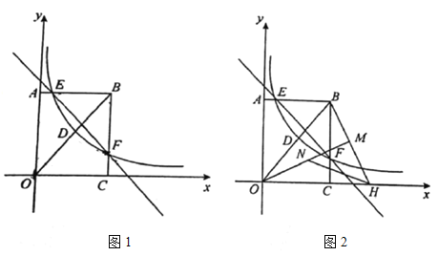
【题目】如图1,在矩形![]() 中,
中,![]() ,分别以
,分别以![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴,建立如图所示的平面直角坐标系,连接
轴,建立如图所示的平面直角坐标系,连接![]() ,反比例函数
,反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,并与矩形的两边交于点
,并与矩形的两边交于点![]() 和点
和点![]() ,直线
,直线![]() 经过点
经过点![]() 和点
和点![]() .
.
(1)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转—定角度,使得点
顺时针旋转—定角度,使得点![]() 的对应点
的对应点![]() 好落在
好落在![]() 轴的正半轴上,连接
轴的正半轴上,连接![]() ,作
,作![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】
(1)连接![]() 、
、![]() ,过点D作DP⊥OC,易得:B(3,4),从而得D(1.5,2),进而得
,过点D作DP⊥OC,易得:B(3,4),从而得D(1.5,2),进而得![]() ,即:
,即:![]() ,E(
,E(![]() ,4),F(3,1),根据割补法,即可求出答案;
,4),F(3,1),根据割补法,即可求出答案;
(2)过点N作NQ⊥OB于点Q,HG⊥OB于点G,易得OH=OB=5,BH=![]() ,HG=BC=4,易证OQN~OMB,得NQ=
,HG=BC=4,易证OQN~OMB,得NQ=![]() ,得到
,得到![]() ,进而得到答案.
,进而得到答案.
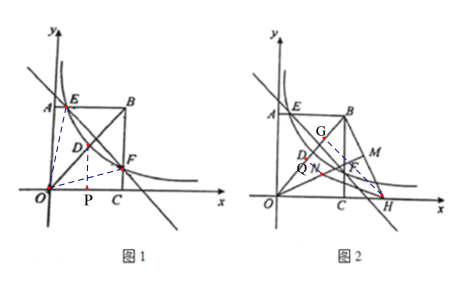
(1)连接![]() 、
、![]() ,过点D作DP⊥OC,如图1,
,过点D作DP⊥OC,如图1,
∵在矩形![]() 中,
中,![]() ,
,
∴B(3,4),
∵点D是OB的中点,
∴DP=![]() BC=
BC=![]() OA=2,OP=
OA=2,OP=![]() OC=1.5,即:D(1.5,2),
OC=1.5,即:D(1.5,2),
∵反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,
,
∴k=xy=1.5×2=3,即:![]() ,
,
∴![]() ,E(
,E(![]() ,4),F(3,1),
,4),F(3,1),
∴BE=3-![]() =
=![]() ,BF=4-1=3,
,BF=4-1=3,
∴![]() ,
,
∴![]() =
=![]()
![]() ;
;
(2)过点N作NQ⊥OB于点Q,HG⊥OB于点G,如图2,
∵线段![]() 绕点
绕点![]() 顺时针旋转—定角度,点
顺时针旋转—定角度,点![]() 的对应点
的对应点![]() 好落在
好落在![]() 轴的正半轴上,
轴的正半轴上,
∴OH=OB=![]() ,
,
∴CH= OH-OC=5-3=2,
∴BH=![]() ,
,
∵![]() ,
,
∴HG=BC=4,
∵![]() ,
,
∴BM=![]() BH=
BH=![]() ,
,
∵∠NOQ=∠BOM,∠OQN=∠OMB=90°,
∴OQN~OMB,
∴![]() ,即:
,即:![]() ,
,
∴NQ=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 的最小值是:4.
的最小值是:4.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
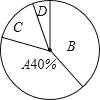
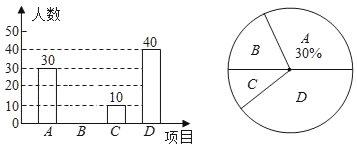
学习实践园地系列答案【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 45~50 | 40 | 0.4 |
B | 40~44 | 42 | x |
C | 35~39 | m | 0.12 |
D | 30~34 | 6 | 0.03 |
合计 | 1.00 |
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.