题目内容
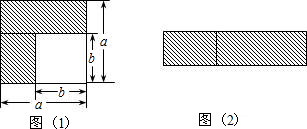
(1)比较左、右两图的阴影部分面积,可以得到乘法公式______(用式子表达).
(2)运用你所得到的公式,计算(a+2b-c)(a-2b-c).

解:(1)(a+b)(a-b)=a2-b2;
故答案为:(a+b)(a-b)=a2-b2.
(2)(a+2b-c)(a-2b-c),
=[(a-c)+2b][(a-c)-2b],
=(a-c)2-(2b)2,
=a2-2ac+c2-4b2.
分析:(1)首先利用平行四边形与正方形面积求解方法表示出两个图形中的阴影部分的面积,又由两图形阴影面积相等,即可得到答案.
(2)利用平方差公式就可简单的计算.注意将a-c看作一个整体.
点评:本题主要考查了平方差公式的几何表示,表示出图形阴影部分面积是解题的关键.注意可以从第2个图形得出平行四边形的高.
故答案为:(a+b)(a-b)=a2-b2.
(2)(a+2b-c)(a-2b-c),
=[(a-c)+2b][(a-c)-2b],
=(a-c)2-(2b)2,
=a2-2ac+c2-4b2.
分析:(1)首先利用平行四边形与正方形面积求解方法表示出两个图形中的阴影部分的面积,又由两图形阴影面积相等,即可得到答案.
(2)利用平方差公式就可简单的计算.注意将a-c看作一个整体.
点评:本题主要考查了平方差公式的几何表示,表示出图形阴影部分面积是解题的关键.注意可以从第2个图形得出平行四边形的高.

练习册系列答案
相关题目