题目内容
如图，△ABC是三边互不相等的三角形．如果要画一个三角形与△ABC全等，且使所画三角形与△ABC的两条边分别在同一条直线上，那么满足上述条件的三角形最多能画出________个．
9
分析：根据三角形全等判定方法，结合已知条件所画三角形与△ABC的两条边分别在同一条直线上，即可得出答案．
解答：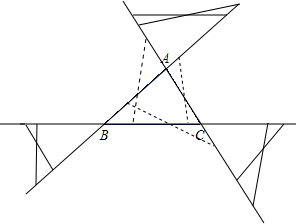
解：如图所示，
①将三条边都向两边延长，分别以每两条延长线为其中两边，每两条延长线为其中两边的三角形构成2个三角形．
有三对延长线，所以有3×2=6个，
②以原来三角形的其中一角作一个新的全等三角形（关于这个角的角平分线对称），这类的三角形有3个，∴△ABC三边不等，有两边在同一条直线上能画出6+3=9个全等三角形与△ABC全等，
即可根据全等三角形的全等条件判断得出答案，满足条件的三角形最多能画出3个．
故答案为：9．
点评：此题主要考查了全等三角形的判定，根据已知延长三角形的各边再作出出符合条件的图形是解决问题的关键．
分析：根据三角形全等判定方法，结合已知条件所画三角形与△ABC的两条边分别在同一条直线上，即可得出答案．
解答：
解：如图所示，①将三条边都向两边延长，分别以每两条延长线为其中两边，每两条延长线为其中两边的三角形构成2个三角形．
有三对延长线，所以有3×2=6个，
②以原来三角形的其中一角作一个新的全等三角形（关于这个角的角平分线对称），这类的三角形有3个，∴△ABC三边不等，有两边在同一条直线上能画出6+3=9个全等三角形与△ABC全等，
即可根据全等三角形的全等条件判断得出答案，满足条件的三角形最多能画出3个．
故答案为：9．
点评：此题主要考查了全等三角形的判定，根据已知延长三角形的各边再作出出符合条件的图形是解决问题的关键．
练习册系列答案
相关题目
3、已知：如图，△ABC是等边三角形，D、E、F分别是三边上的中点，则和△ABD全等的三角形有（ ）个（除去△ABD）．
9、如图，△ABC是三边互不相等的三角形．如果要画一个三角形与△ABC全等，且使所画三角形与△ABC的两条边分别在同一条直线上，那么满足上述条件的三角形最多能画出
8、如图，△ABC是等边三角形，AD、BE、CF分别是三边的中线，则图中有几类全等的三角形（不同形状的）（ ）
