Question

【题目】如图，在平面直角坐标系中，抛物线经过B（3，0），C（0，-3）两点，点D为顶点．

（1）求抛物线的解析式及顶点D的坐标；

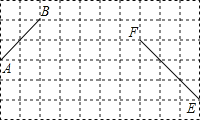
（2）点E在抛物线的对称轴上，F在BD上，求BE+EF的最小值；

（3）点P是抛物线第四象限的点（不与B、C重合），连接PB，以PB为边作正方形BPMN，当点M或N恰好落在对称轴上时，求出对应的P点的坐标（结果保留根号）．

Answer 1

【答案】（1），D（1，-4）；（2）；（3）或

【解析】

（1）把B、C点的坐标代入抛物线方程，利用待定系数法，可以把方程中的未知数求解出来，从而得到抛物线的表达式，把解析式整理成顶点式，即可得到顶点D的坐标；

（2）利用对称轴的性质，知道AE=BE，从而把BE+EF的长度转换成AF的长度，求出BE+EF的最小值；

（3）利用全等三角形的性质，根据已知线段可求得相应坐标.

解：（1）把B、C点的坐标代入抛物线方程得到：

解得

∴表达式为，

又∵，

所以顶点的坐标为D（1，-4），

（2）如图1，连接BD，过A作AF⊥BD于F，交对称轴于点E，

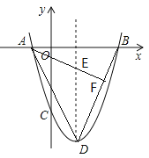
图1

∵E点在抛物线的对称轴上

∴AE=BE

则BE+EF=AE+EF=AF

又因为两点之间垂线段最短

所以所做的AF为所求的最小值

由三角形的面积公式可以得到 (h是三角形ABD以AB为边的高)

又由题意可知，，

所以，

因此：，

∴BE+EF的最小值为.

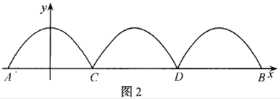
（3）当点N在对称轴上时，如图2，过点P作PF⊥OB于点F，

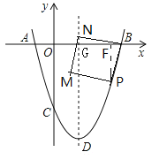
图2

∵四边形PBNM是正方形 ， ∴，

又∵，∴，

在和中

∵

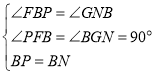
∴(AAS)，

∴ ，

设点P的坐标为（），则，整理得

解得：，（舍去）

∴

当点M在对称轴上时，如图3，过点P作PG⊥OB于点G，过点P作PF⊥MD于点F，

同理可证：，∴

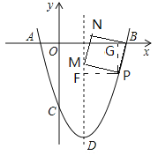
图3

设，代入得，

解得：，（舍去）

当时，，

综上所述：对应的P点的坐标有或