Question

（2011•天门三模）有一只圆柱形茶杯，在茶杯的外侧A处有一只可爱的小蚂蚁，它到杯子口C点的距离为6cm，在茶杯的内侧B处有一块糖果，它到杯子口D点的距离为2cm，C、D两点间的弧线长为6cm，请你帮小蚂蚁算一算，最短要走

10

cm才能吃到糖．

Answer 1

分析：如图，延长BD，在延长线上取点B'，使BD=B'D=2cm，连接AB'，交CD与点E，连接BE，则最短的路线应该是沿AE、EB爬行即可．因为两点之间线段最短，最后利用勾股定理即可求解．

解答：解：如图，延长BD，在延长线上取点B'，使BD=B'D=2cm，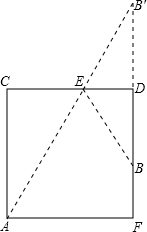
连接AB'，交CD与点E，连接BE，
则最短的路线应该是沿AE、EB爬行即可．
因为两点之间线段最短．
在△AB′F中，∠F=90°，AF=CD=6cm，B′F=6+2=8cm，
由勾股定理，得AB′=10cm．
∵ED⊥BB′，
∴BE=B′E，
∴AE+BE=AE+B′E=AB′=10cm，
∴小蚂蚁最短要走10cm才能吃到糖，
故答案为：10．

点评：本题主要考查平面展开-最短路径问题，解题关键是根据题意确定最短路线，解此类题目的一般思路是先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．