Question

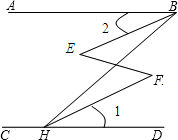如图，已知：∠E=∠F，∠1=∠2，试说明：∠ABH+∠CHB=180°．

Answer 1

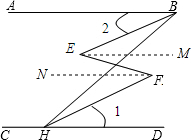证明：过点E作EM∥AB，过点F作FN∥CD，
∴∠2=∠BEM，∠1=∠HFN，
∵∠BEF=∠EFH，∠1=∠2，
∴∠BEF-∠BEM=∠EFH-∠HFN，
∴∠MEF=∠NFE，
∴EM∥FN，
∴AB∥EM∥FN∥CD，
∴∠ABH+∠CHB=180°．
分析：首先过点E作EM∥AB，过点F作FN∥CD，由：∠E=∠F，∠1=∠2，易证得∠MEF=∠NFE，由平行线的判定，可得EM∥FN，继而可得AB∥EM∥FN∥CD，然后由平行线的性质，即可证得：∠ABH+∠CHB=180°．
点评：此题考查了平行线的判定与性质．此题难度适中，注意掌握辅助线的作法是关键，注意数形结合思想的应用．